2. Lexical Analysis
Angold Wang 19/02/2022
User view
if (i == j)
z = 0;
else
z = 1;Compiler view
if (i == j)\n\t\tz = 0;\n\telse\n\t\tz = 1;1. Formal Languages
Seperate Syntax and Semantics
- Makes clear what is syntax, what is semantics.
- Example: Roman numerals vs. Arabic numerals
- Roman numerals are painful to do addition and subtraction, etc.
- The reason is that the algorithms were kind of complicated.
- The notation causes this big difference (procedure)
- Don’t underestimate the importatance of notation.
Syntax vs. Semantics
- We can use Multiple syntax to represent the same semantics.
- Which is the basis of Optimization.
- The fact that several programs that are actually functionally equivalent, that allow us to substitute one program that runs faster than another.
- Never one to many!!!
2. Lexical Specification
1. Write rexp for the lexemes of each token class
- Number = digit+
- Keyword = ‘if’ + ‘else’ + ‘for’ + …
- Identifier = letter(letter + digit)*
- OpenPar = ‘(’
- …
2. Construct R, matching all lexemes for all tokens
Which is just the union of all the regular
expressions
R = Keyword + Identifier + Number + ...
R is the some of of all the different token classes of our
language
3. Let input be x1...xn
For 1 <= i <= n check whether
x1...xi in L(R).
What if no rules matches? * if the whole
x1...xn not in L(R) - We don’t let this ever
happen. * We we are going to do instead, is to write a category
of error strings. *
ERROR = all strings not in the lexical specifications
* Put ERROR last in piority
4. If success, then we know that
x1...xi in L(Rj) for some
j
How much input is used? * if
x1...xi in L(R), and so as
x1...xj (i != j) * For example.
== should be treat as “double =” or
“equal operator ==”? * Solution: Maximal
Munch * We should always take the longer one when meet
ambigurity * That just the way that humans themselves read things
Which token is used? * Suppose
R = R1 + R2 + ... Rn and there we have: *
(x1...xi) in L(Rj) * (x1...xi) in
L(Rk) * k != j * For example.
if should be treat as an Identifier or a
keyword? * Solution: Piority Ordering * Choose
the one listed first. * typically, put keywords before
the identifiers
5. Remove
x1...xi from input and go to (3)
3. Finite Automata
- Regular expressions = specification
- Finite automata = implementation
- Both NFAs and DFAs can recognize regular languages (equivalent power)
- DFAs are faster to execute.
- There are no choices to consider
- NFAs are, in general, smaller.
Example: A NFA that accepts the rexp:
1* + 0:
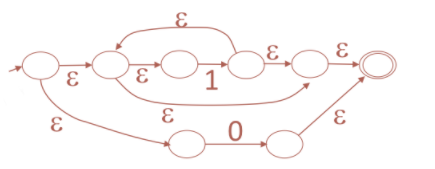
1. Regular Expressions -> NFA
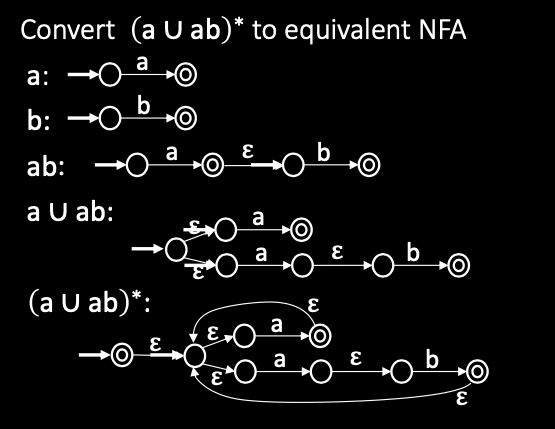
2. NFA to DFA
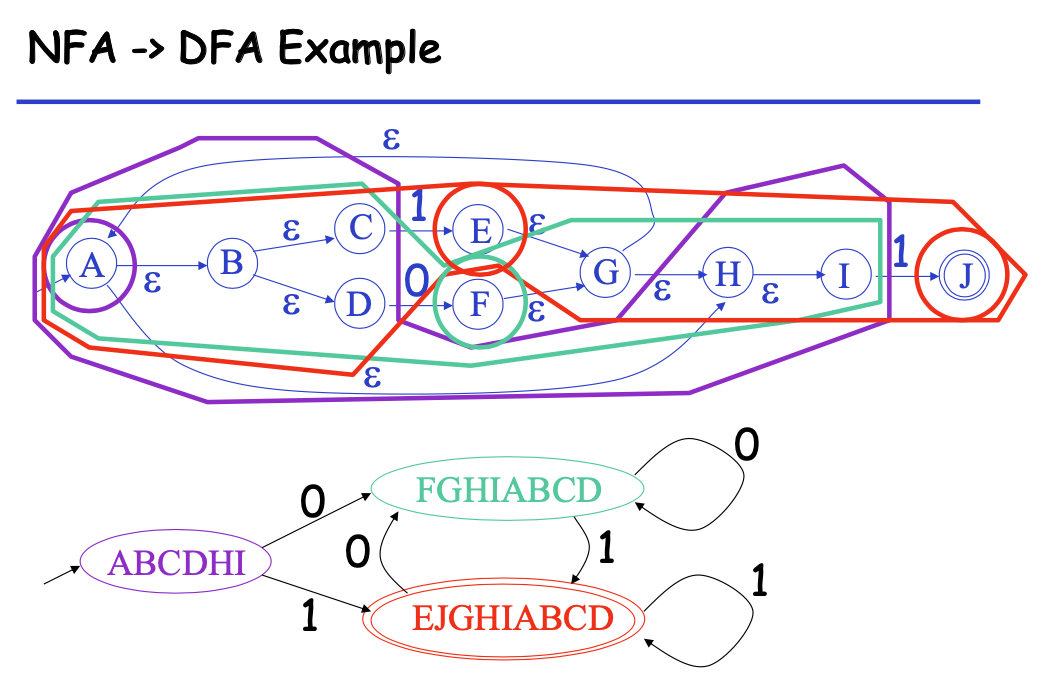
- Key IDEA: DFA M’ keeps track of the subset of possible states in NFA M.
- That is why in general DFA are much bigger:
2^n - 1subsets for n states NFA
3. Implement Table-driven DFA
3. Exercises
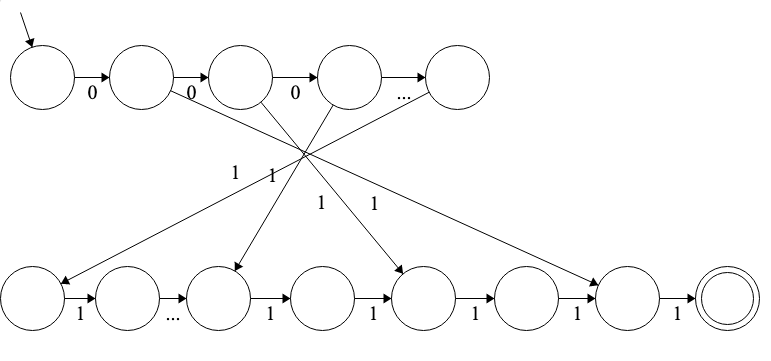
1. Minimum States

- Answer: Minimum states: 3n + 1
2. NFA vs. DFA
Question: Which of the following automata are NFAs?
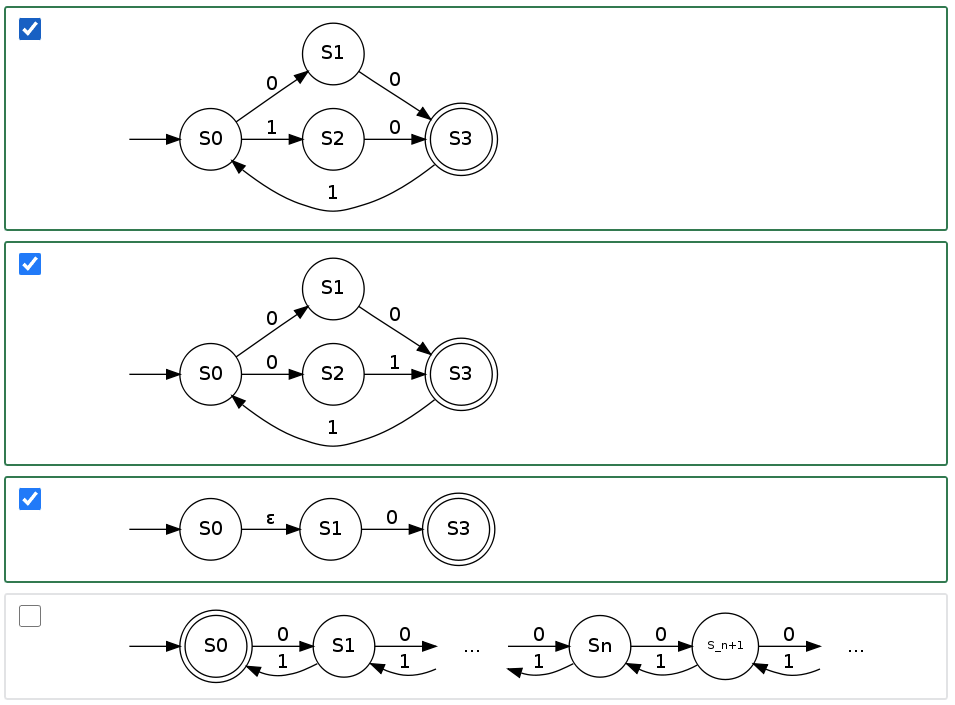
- NFAs must have a finite set of states, which rules out the last option.
- Every DFA is also an NFA, which is why the first option is included.