Angorithm4 Webinar #4

Cohost by Jiawei Wang 2021-11-5

1. Main Falcon

2. Comparision Sort(II) - QuickSort

i. Description

The Quicksort algorithm has a worst-case running time of O(N^2) on any input array of number.

Despite this slow worst-case running time, Quicksort is often the best practical choice for sorting because it is remarkbly efficient on the average: Its expected running time is O(nlogn) and the constant factors hidden in the O(nlogn) notation are quite small.

• Designed by Hoare in 1962
• Sort in Place (No extra storiage needed)
• Three or more times faster than Merge Sort (Merge guarentee O(N))
• Most good sorting algorithms that you will find are based on quicksort
• But not the Theoretically fastest sorting algorithm (Will be proved in the next Webinar)

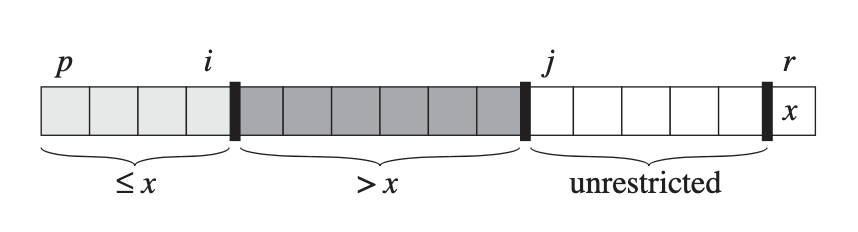
int Partition(vector<int> &A, int p, int q) {
    // (p, i) (i+1, j)
    int x = A[p];
    int i = p;
    for (int j = p + 1; j <= q; j++) {
        if(A[j] <= x) {
            i = i + 1;
            swap(A[i], A[j]);
        }
    }
    swap(A[p], A[i]);
    return i;
}


void QuickSort(vector<int> &A, int p, int r)  {
    if (p < r) {
        int q = Partition(A, p, r);
        QuickSort(A, p, q-1);
        QuickSort(A, q+1, r);
    }

}

• Partition(A, p, q) find the rank of A[p] in region [p, q]
• Initial call: QuickSort(A, 0, n-1)

  5   2   6   1
  5   2   1   6
  1   2   5   6

ii. Analysis

Key: Good / Bad Partition

1. Worst-Case Partitioning

The worst-case behavior for quicksort occurs when the input is sorted or reverse-sorted.
At that time, the partition routine produce one subproblem with n-1 element and one with 0 element

T(N) = T(N-1) + O(N) -> O(N^2)

2. Best-Case Partitioning

• When Best-Case ?

Back to 1. Worse-Case
T(N) = max(T(q) + T(N-q-1)) + O(N)

We use substitution method, asssume that T(N) <= cN^2 for some constant c

T(N) <= max(c q^2 + c (n-q-1)^2) + O(N)
T(N) <= c max(q^2 + (n-q-1)^2) + O(N)
f'(q) = 4q - 2n + 2
f''(q) = 4 -> f'(q) = 0 when q = n/2 - 1/2 = (n-1)/2 and that time get the minimum

Which subproblem’s size no more than n/2 T(N) = 2T(N/2) + O(N) -> O(NlogN)

3. Randomized Quicksort -> proof the avg Time Complexity is O(NlogN)

iii. Example (LeetCode 215)

nums = [3,2,1,5,6,4], k = 2
Output: 5

using namespace::std;

class Solution {
public:
    // #1 using priority queue
    int findKthLargest(vector<int>& nums, int k) {
        priority_queue<int> q(nums.begin(), nums.end());
        for (int i = 0; i < k - 1; ++i) {
            q.pop();
        }
        return q.top();
    }

    // #2 using quick sort partition
    int findKthLargest2(vector<int>& nums, int k) {
    int left = 0; int right = nums.size() - 1;

    while (true) {
        int desc = Partition(nums, left, right);
        
        if (desc == k-1) 
        return nums[desc];

        if (desc < k-1) {
        // nums[pos-1] is too large
        left = desc + 1;
        } else {
        right = desc - 1;
        }
    }
    }

private:
    int Partition(vector<int> &A, int p, int q) {
    // [p, i] [i+1, q]
    //  ----------->
    // descending order
    int x = A[p];
    int i = p;
    for (int j = p + 1; j <= q; j++) {
        if(A[j] >= x) {
        i = i + 1;
        swap(A[i], A[j]);
        }
    }
    swap(A[p], A[i]);
    return i;
    }
};