Angorithm4 Webinar #3

Cohost by Jiawei Wang 2021-10-29

1. Review ISC

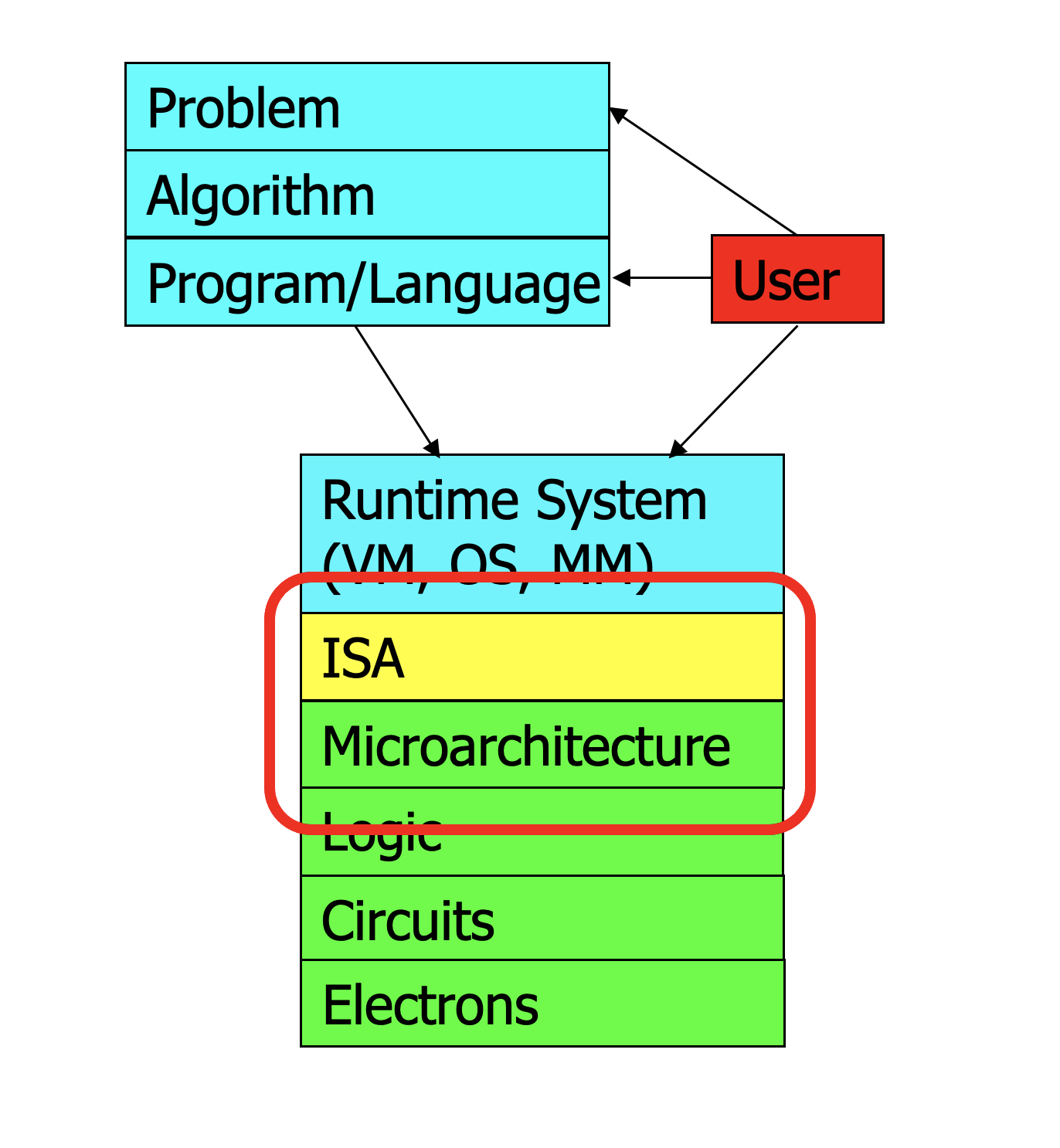
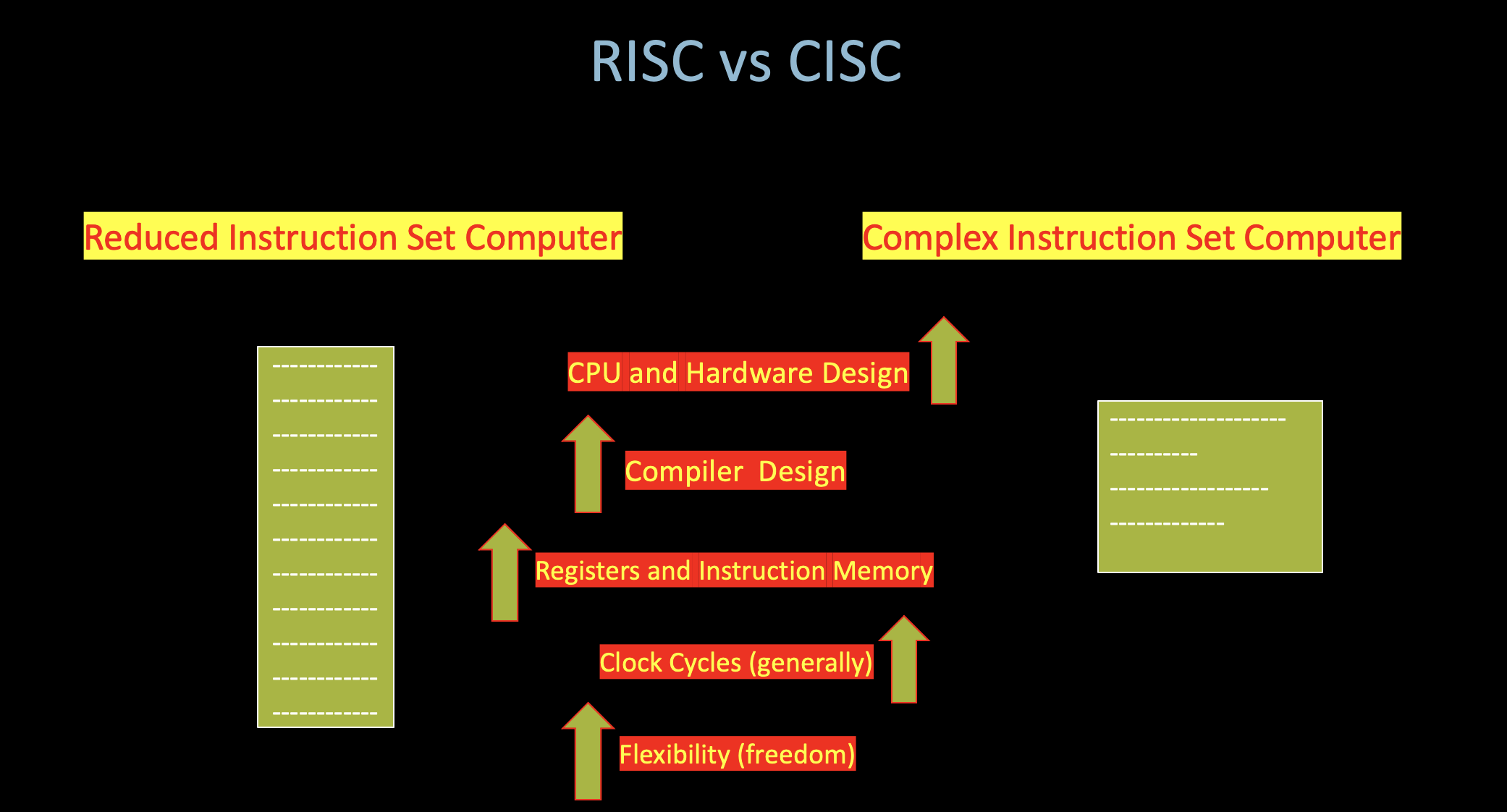
Trade off

In 1981s. Compiler technology didn’t develop well at that time.
Simple Compiler, Complex Hardware vs. Complex Compiler, Simple Hardware

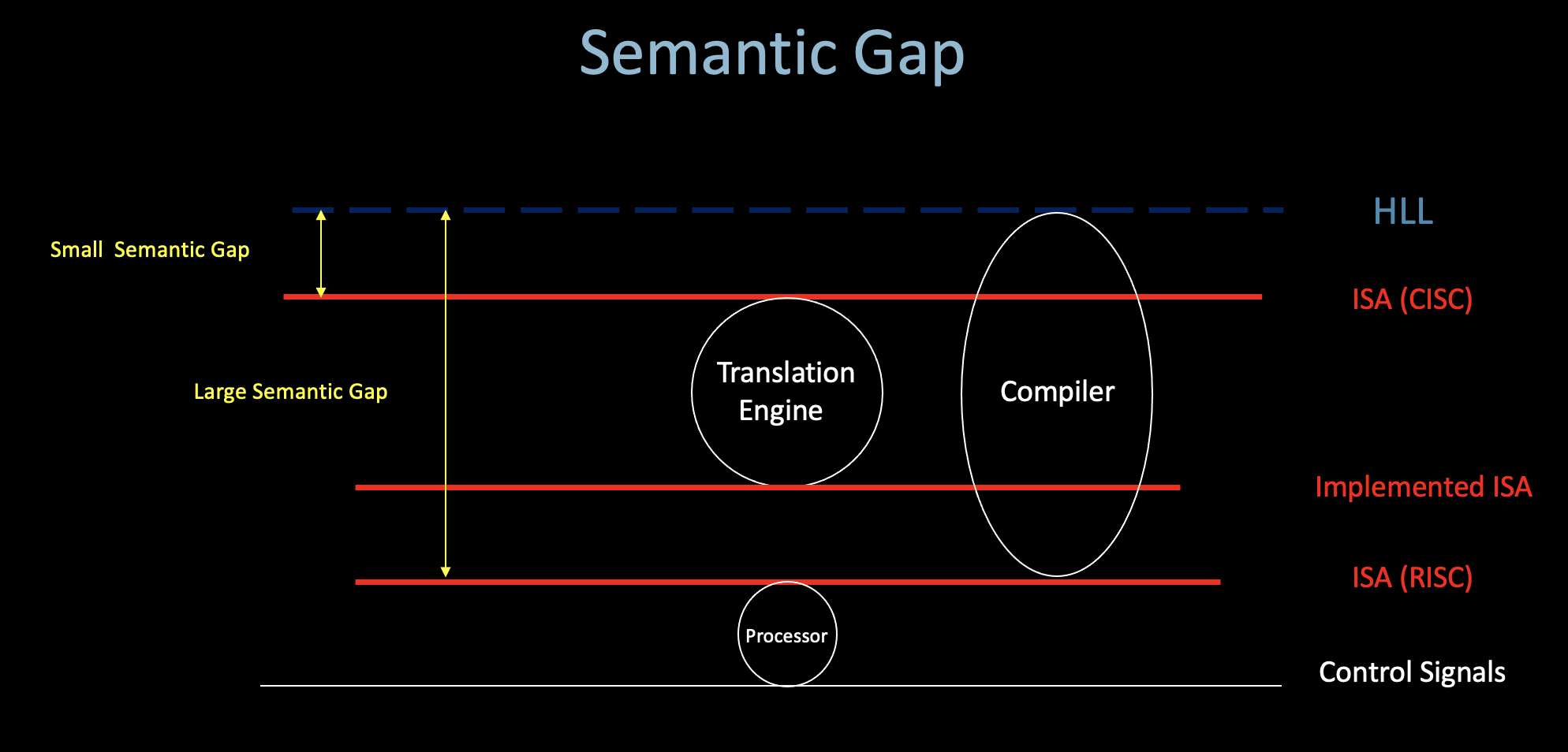semantic ### Decode in x86: * Intel’s and AMD’s x86 implementations translate x86 instructions into programmer-invisible microoperations (simple instructions) in hardware * In fact, in most x86-64 machines today, what’s the processors do is that they take the complex instructions, they translate down, and save the translated form, so next time, when you get the same instruction, you don’t need to translate it again. You just take the simple micro-operations. * All high-performance processors’ underneath looks like RISC processors

2. Comparision Sort(I) - Merge Sort

i. Description


void Merge(int* A, int* L, int leftCount, int* R, int rightCount) {
    int i, j, k;
    i = 0, j = 0, k = 0;

    while (i < leftCount && j < rightCount)
    {
        if(R[j] < L[i]) A[k++] = R[j++];
        else A[k++] = L[i++];
    }

    // last check
    while (i < leftCount) A[k++] = L[i++];
    while (j < rightCount) A[k++] = R[j++];

}

void MergeSort(int* A, int n) {
    int mid, *L, *R;

    if (n < 2) return;

    mid = n / 2;

    L = new int[mid];
    R = new int[n - mid];

    for(int i = 0; i < mid; i++) L[i] = A[i];
    for(int j = mid; j < n; j++) R[j-mid] = A[j];

    MergeSort(L, mid);
    MergeSort(R, n-mid);

    Merge(A, L, mid, R, n-mid);

    delete [] R;
    delete [] L;

}

      5     2     6     1

   |  1     2     5     6  |     
   |  2     5  |  1     6  |
   |  5  |  2  |  6  |  1  |

ii. Analysis

T(N) = 2T(N/2) + O(N)

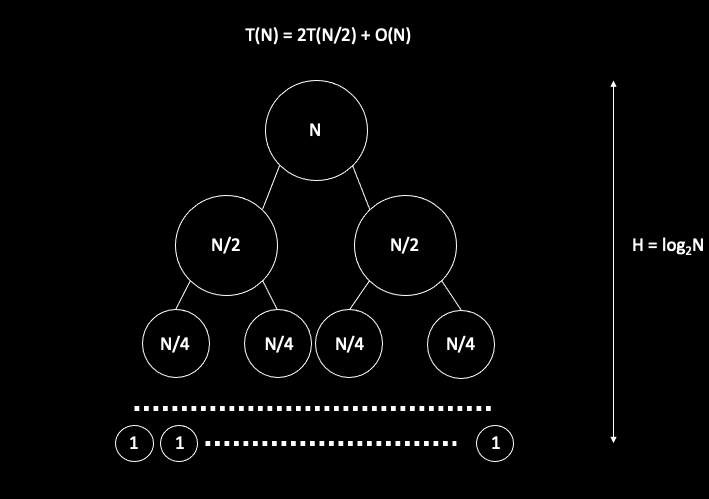
`O(NlogN)`

iii. Example (LeetCode 315)

LeetCode 315 Count Number of Smaller Numbers After Self

Input:  [5,2,6,1]
Output: [2,1,1,0]

class Solution {
public:
    vector<int> countSmaller(vector<int>& nums) {
        for (int i = 0; i < nums.size(); i++) {
            int count = 0;
            for (int j = i+1; j < nums.size(); j++) {
                if (nums[j] < nums[i]) count++;
            }
            nums[i] = count;
        }
        return nums;
    }
};

Divide and Conquer

[A A A A A  B B B B B]
[A A A A A][B B B B B]

[X X X X]

using namespace::std;

class Solution {
    vector<int> counts;
public:
    vector<int> countSmaller(vector<int>& nums) {
        int N = nums.size();
        counts.resize(N);

        if (N == 0) return {};

        vector<int> sortedNums = nums;

        helper(nums, sortedNums, 0, N-1);

        return counts;
    }

private: 
    void helper(vector<int>& nums, vector<int>& sortedNums, int start, int end) {
        if (start == end) return;


        int mid = start + (end - start) / 2; // round down ((int) x / 2 <= (float) x / 2)
        helper(nums, sortedNums, start, mid);
        helper(nums, sortedNums, mid+1, end);

        for (int i = start; i <= mid; i++) {
            auto iter = lower_bound(sortedNums.begin() + mid + 1, sortedNums.begin() + end + 1, nums[i]); // [mid+1, end+1)
            counts[i] += iter - (sortedNums.begin() + mid + 1); // Ranking in [mid+1, end]
        }
        
        vector<int> temp(end - start + 1); // to store the merged vector from start to end
        // sort(sortedNums.begin()+start, sortedNums.begin()+end+1);

        int i = start, j = mid+1, p = 0;
        while (i <= mid && j <= end) {
            if (sortedNums[i] <= sortedNums[j]) {
                temp[p] = sortedNums[i];
                i++;
            } else {
                temp[p] = sortedNums[j];
                j++;
            }
            p++;
        }

        while (i <= mid) {
            temp[p] = sortedNums[i];
            i++;
            p++;
        }

        while (j <= end) {
            temp[p] = sortedNums[j];
            j++;
            p++;
        }

        for (int i = 0; i < end-start+1; i++) {
            sortedNums[start+i] = temp[i];
        }

    }
};

Runtime

      5     2     6     1

   |  1     2     5     6  |  <- counts = [2, 1, 1, 0]
   |  2     5  |  1     6  |  <- counts = [1, 0, 1, 0]
   |  5  |  2  |  6  |  1  |  <- start == end return